Straight into it:
SWOON.
I might have given a spoiler alert: that was the “top of the mountain” of a piece I’m hoping you’ll listen to all of.
This excerpt is something of a climactic moment from the final variation of Ben Johnston’s String Quartet No. 4 (Amazing Grace). The performers here are the Kepler Quartet, who, in a heroic fourteen-year effort, managed to record and release all ten of Johnston’s quartets, across three albums. Recently I was very excited to find an overview of this work (and discussion of the passage above) in Kyle Gann’s 2019 book The Arithmetic of Listening.
The first thing commonly said about this piece is that it is “one of the most difficult string quartets ever written.” Yeah okay, fine. I strongly prefer how Gann introduces it:
Ben Johnston’s Fourth String Quartet (1973) is one of the most beloved of microtonal works, a rare avant-garde piece that has found, and can thrill, a wide audience.
True story. If you’ve never heard this piece, push play and get ready for that thrilling, emotionally transformative ride:
I acquired the score (just eighteen spiral-bound 11x17 pages) after this recording left me absolutely dumbstruck with ecstasy. I threw it on the top of my “score-study to-do” pile and there it sat, for a year… staring… just daring me to mess with it.
Every time I put my mind to studying Johnston’s music, it pays off, big time,1 and I knew this would be no different. So I was really excited to discover Gann’s overview, which precipitated my finally diving in.
Here’s what happened:
Three measures
For the purposes of this example the notes below aren’t the point, so feel free to just like, glide over them. They look complex, and that’s because, omg, they absolutely, 1000% are… for the performer. But for the listener or theorist (that’s #us), they are actually delightfully and beautifully elegant when put in the right light (that’s #thelattice).
SO:
How on earth do I make sense of the following passage:
There are more than twelve notes here, none of which you’ll find on the piano keyboard.2 They are part of a collection that Gann intimidatingly refers to as a…
… hyperchromatic scale … the first violin plays it at the climax. After this ecstatic rendering, the rhythmic complexities and pitches gradually diminish and fall away until the music ends up in a gentle cadence …
In a nutshell, this example is being given to show the way nearly the full complement of pitches that have been built up over ten minutes are used, all at once, in the emotional climax of the work.
Looking at a passage like this, I immediately wanted to know:
What are these pitches!?
How are they related: to each other, and to the piece as a whole?
I guess I could start by… alphabetizing them? 🤷♂️
Huh.
We don’t need lattice, we already have notation at home.
If you’ve spent a lot of time in music theory classes, you probably expect that if you can
catalogue all the notes used in a passage,
put them in order from low to high3, and
figure out which one feels like “home,”
… then you’ll reveal a familiar “scale.” Without further exploration, you expect that you’ll immediately know… something… about a passage.
You might be trying to analyze some music, and you might be all 🤔 and then you follow these steps and then…
“Ah, G-Flat Super Locrian!" ☝️🤓, you might say. A fine scale.
Huh!
If, like me, you’re from musical outer space, you might have been a little confused in music theory class by these names: Major, Minor, Dorian… and how they are visualized in notation.
You might have asked:
“if all the ‘major’ scales have the same quality of sound and the same order of intervals, how come they all look different on the page!? This passage over here has one sharp, that one over there has four flats. How can they both be “major?”
“Sometimes even the same music looks different on the page depending on who’s part you’re looking at? Like… why does our bass clarinetist get two sharps and I get none!? Is she better at music than me?
I have an idea: wouldn’t it make more sense if, say, all the ‘major’ scales had no accidentals? Maybe then we give all the ‘lydian’ scales one sharp, the ‘minor’ could have three flats and ‘dorian’ could have two. Wouldn’t that make more sense?”
- Chris P Thompson, Remedial Music Theory “A,” 1997.
This is what happens when you take a drummer out of the drum corps and sit him down in a conservatory music theory class.
I’m being facetious (kind of!), but with a point, and the point is this:
While staff notation is good at efficiently showing us what keys to push on a piano, it isn’t always the clearest or most intuitive way to visualize the relationships we perceive between the pitches we’re hearing.
And, oh boy, what happens if you suddenly realize that there aren’t just twelve, but an infinite number of pitches to choose from? And none of them are on your piano? Squeezing scales with twenty, or fifty-three, or a thousand4 pitches into staff notation gets even more convoluted, and starts to show how specialized (and limited?) that notational system actually is:
Here’s what those pitches sound like, in order:
Huh. Well, we’ve arranged them from low to high. It’s still not telling us much?
I still want to know: how they are related.
Are they even related?
Speaking in ratios
Those note names with all the strange accidentals — they’re just a (very elegant, all things considered) system of translating ratios into the awkward framework of staff notation. But in his analysis, Kyle Gann very helpfully provides the ratios5 above each pitch:
Hey look, it’s “1/1” — could that be our “tonic?”
Learning to think and speak in ratios gets us one step closer to the real relationships in music… what we actually perceive. To our ears a 3/2 ratio is a 3/2 ratio no matter where it lives. Demonstrating this has been the point of the past few weeks of posts.
Gann really saved me a step in my quest for knowledge here. It’s with those ratios that I was able to very quickly build this piece’s lattice.
The lattice
This is where I get to stop using so many words, forget all those note names, accidentals, and even ratios… and let the lattice show us: how this very complex-looking score is built from simple, familiar relationships:
When it comes to analysis, especially for just intonation, the lattice is a the clearest (and, I would argue, most beautiful) way to visualize relationships between frequencies. Exploring a portion of the lattice reveals the way our perception of the composer’s palate is organized.
This makes it massively powerful for anyone composing or analyzing music.
And not just to composers, but performers and listeners as well. Seeing the natural proportions of the elements of a piece of music (even if only in the abstract), enriches the experience.
Afterword
As this piece comes to a close, how consciously aware are you that you’re hearing a “microtonal” work? Not at all? Enough to be intrigued, or scared away? To the extent that you were able to perceive it as microtonal, did that quality enhance the emotional effect?
To me (and many others) Johnston’s fourth quartet is a watershed moment for the compositional practice it represents. Whether you call that practice “microtonality” or “just intonation” or something broader,6 the piece is proof-of-concept for the universal emotional power of its materials.
I love that it expects nothing of you other than your humanity, and assumes no knowledge other than maybe a little bit of cultural context.
It teaches you about its world as it goes.
Continue on to Part V, which gets a little Monty Python, ngl:
🔉👋 Subscribe for free:
Six months ago I set out to find out what was happening in one short passage from the ninth quartet, where I could have sworn the music was like… melting?
What I found in that excerpt was so elegant and intentional and effective that I couldn’t help but share it, even though I hadn’t yet sufficiently introduced the idea of the lattice here. So I had to dance around that a bit.
You might be looking at that “A,” with no accidental attached, but even that “A” is a different “A” from the one on the piano, because of the scordatura tuning of the strings.
I’d like to also point out: organizing pitches from “low” to “high” is the same as organizing their frequencies from “slow” to “fast.” Just saying.
You might assume I’m exaggerating. Johnston’s String Quartet No. 7 has more than twelve hundred pitches to the octave. And you know what… as difficult as it is for the performers, it’s organized, intentional, emotionally effective… stunning.
Just to clarify/refresh: those are the ratios between the actual frequencies. Our brains do that math subconsciously, and feed us intuitive sensations, such that we recognize ratios as different musical intervals.
I will never stop screaming that a) I think this is amazing, miraculous even and b) I just find it really sad that western music theory completely ignores ratios in its approach to analyzing music.
I haven’t even mentioned the fact that this piece uses the same ratio relationships of its pitches for its rhythmic content as well. I tend to think of the just intonation approach to more than just pitch, but also to rhythm, tempo, phrase, and formal structure as “rational music theory.”






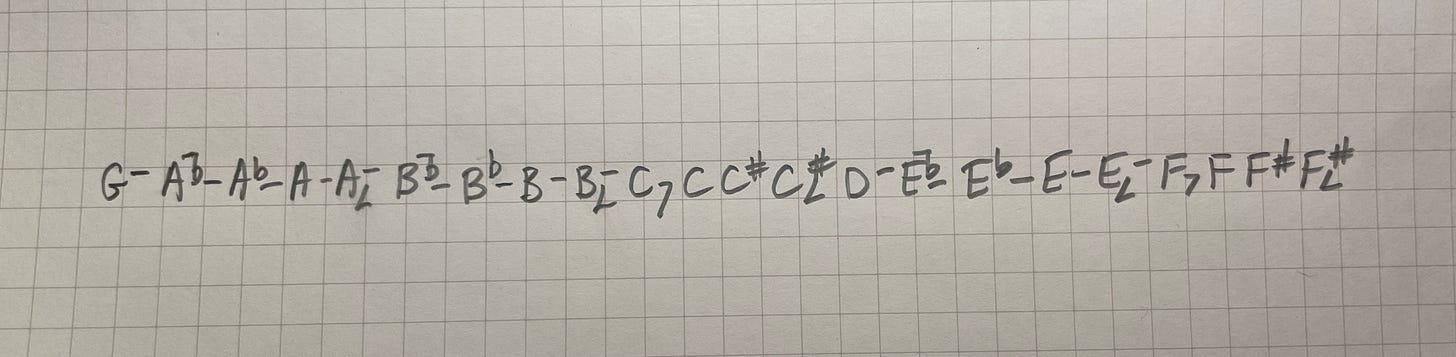



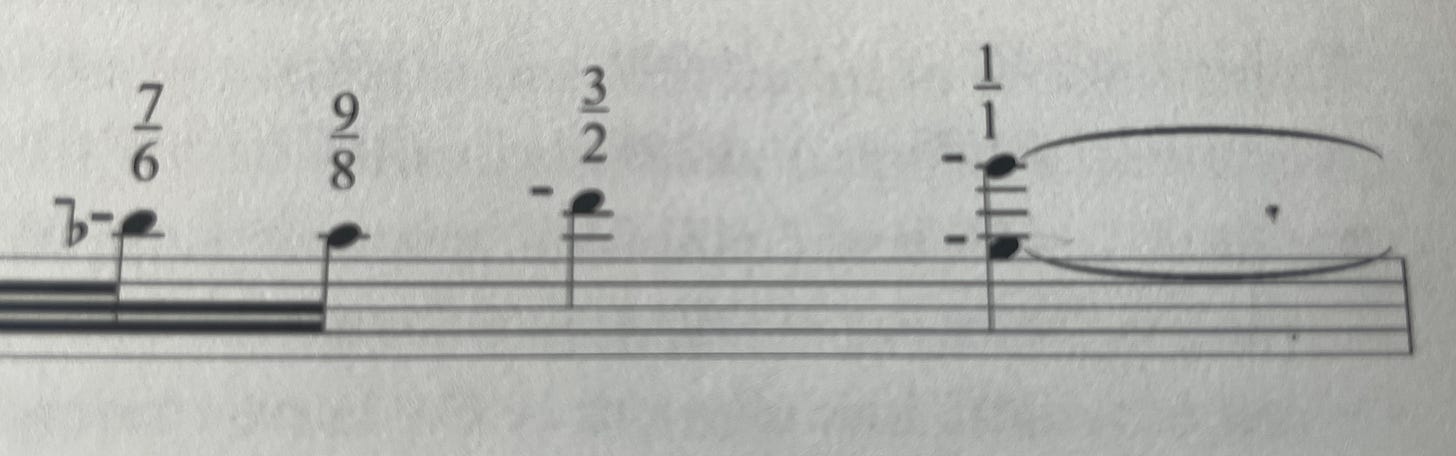

Inspiring and brilliant, as always.
Please keep these amazing weekly feasts coming, Chris.