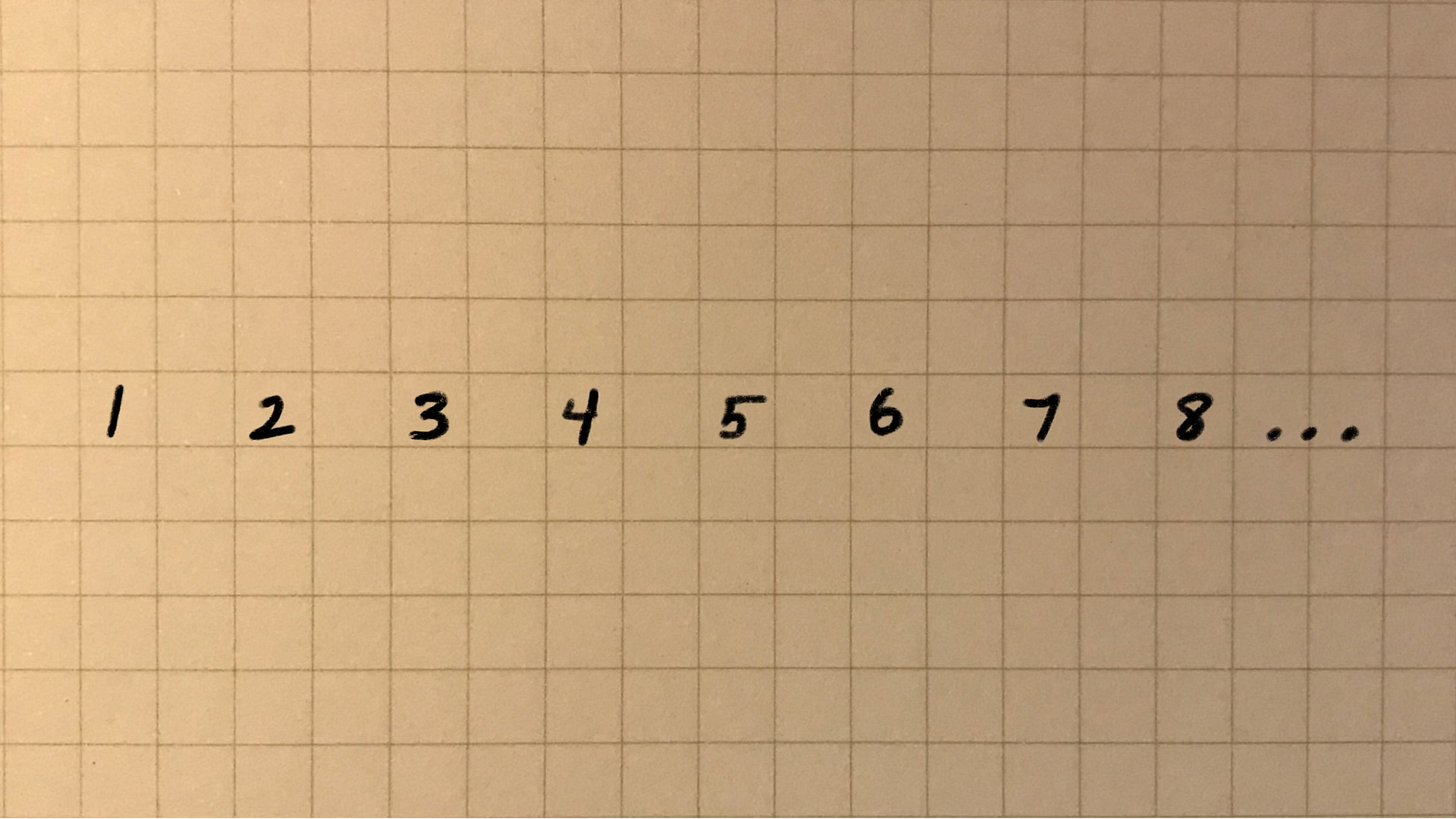Harmonic
One must have a sequence.
🚪👋 Hello. I’m visiting everyone in this neighborhood with an important message. I have something to share with you about the wonderful things that The Harmonic Series will do for mankind. Is one familiar with The Harmonic Series?
No doubt one is a busy person, so I’ll be brief:
Some people to whom we talk have confidence in The Harmonic Series. Others find it difficult to believe in. How do you feel? . . . The Harmonic Series encourages us to consider the significance of the physical universe. The laws governing the heavenly bodies provide valuable direction for us.
Would you like to know what one’s harmonic series looks like?
1️⃣☝️ Fundamental
People get all spiritual about the harmonic series: it shows up all over the natural world, is the backbone of musical timbre, and can be represented in beautiful, elegant ways that feel positively divine: like glimpses of a higher power.
But ultimately it’s just a simple concept from pure math: a sequence of numbers.
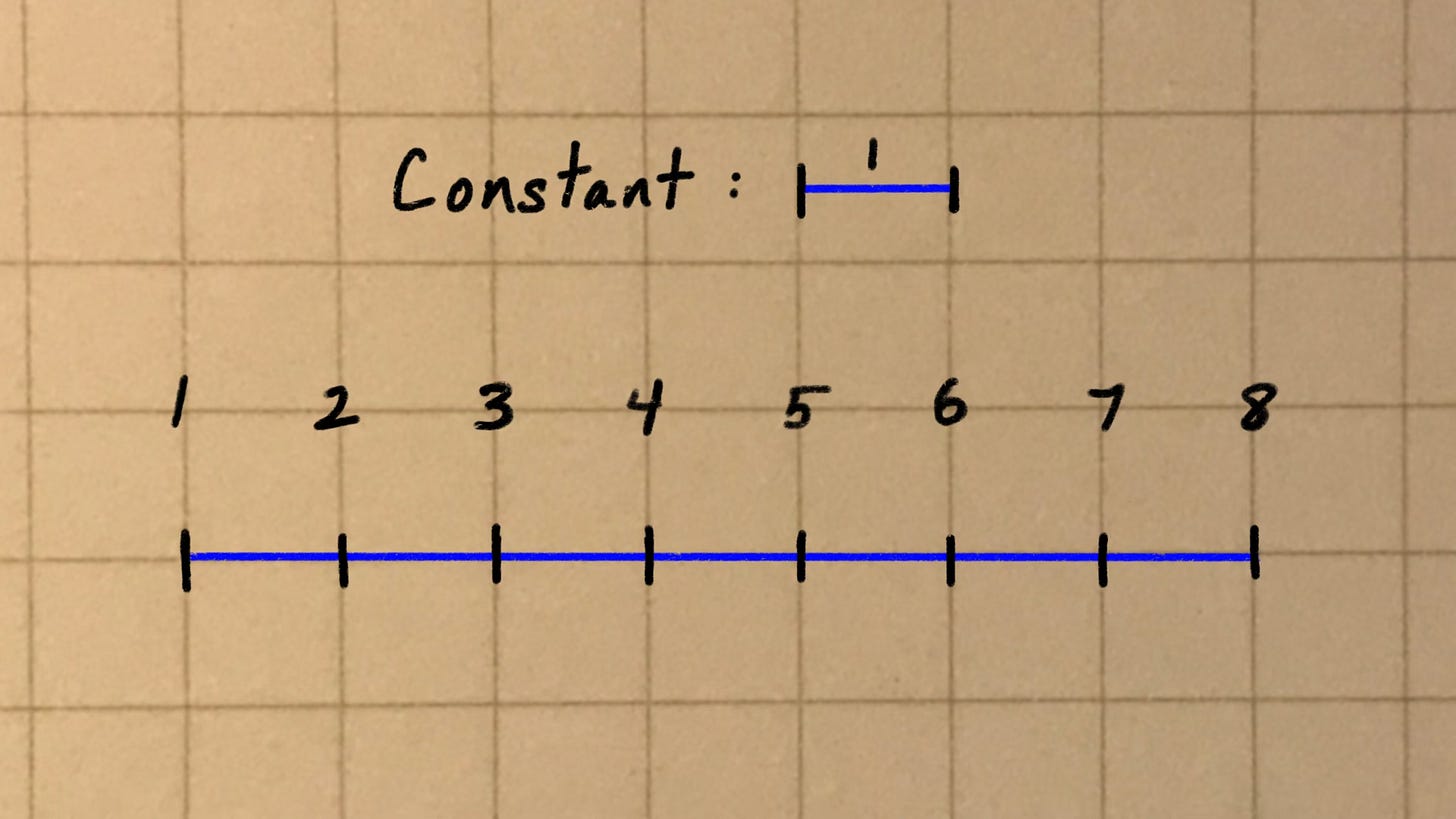
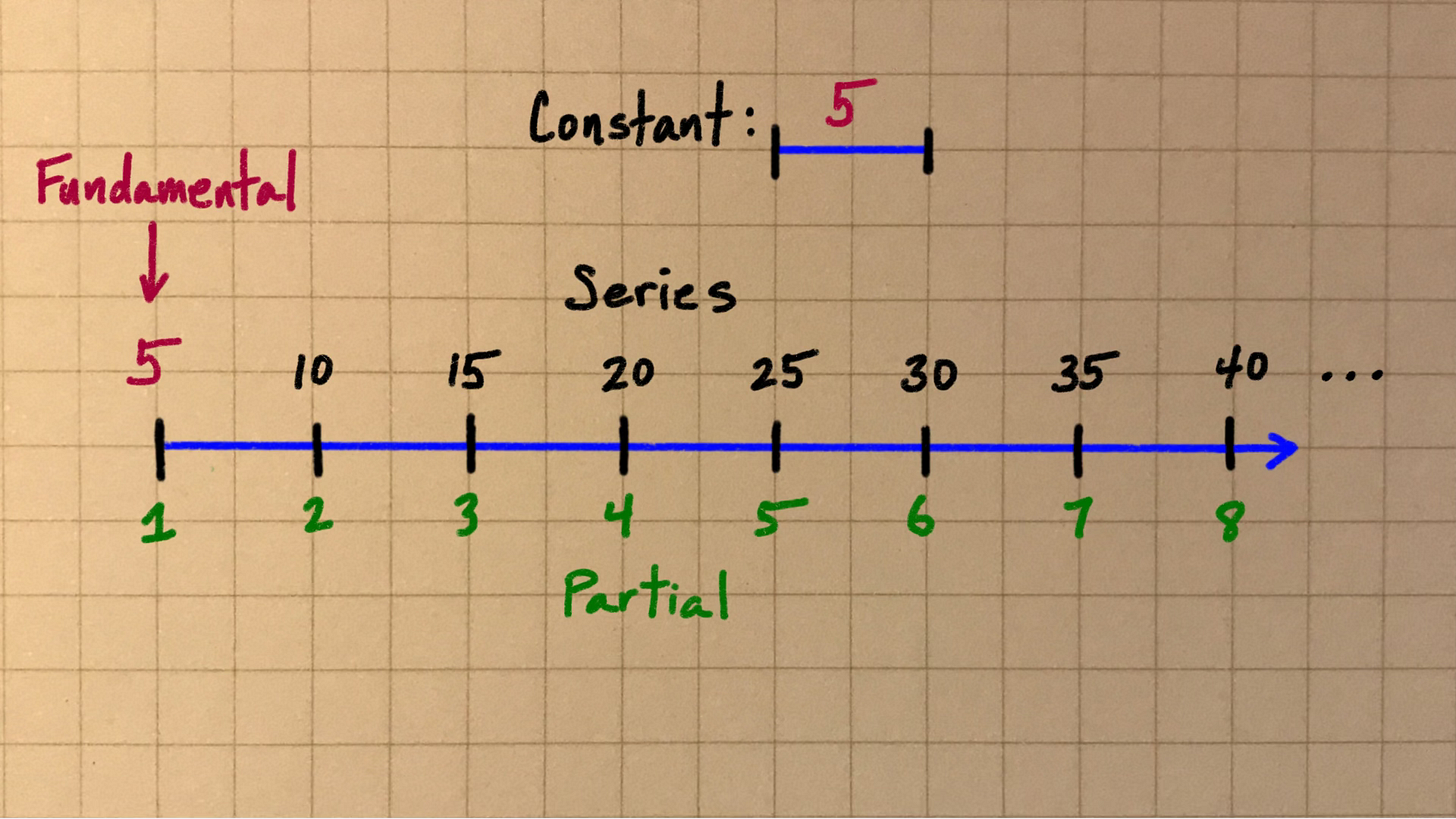
You might first encounter “sequences” in Algebra I, when the subject of “arithmetic” sequences are introduced. What makes a sequence of numbers “arithmetic?” — when the difference between each successive number is constant:
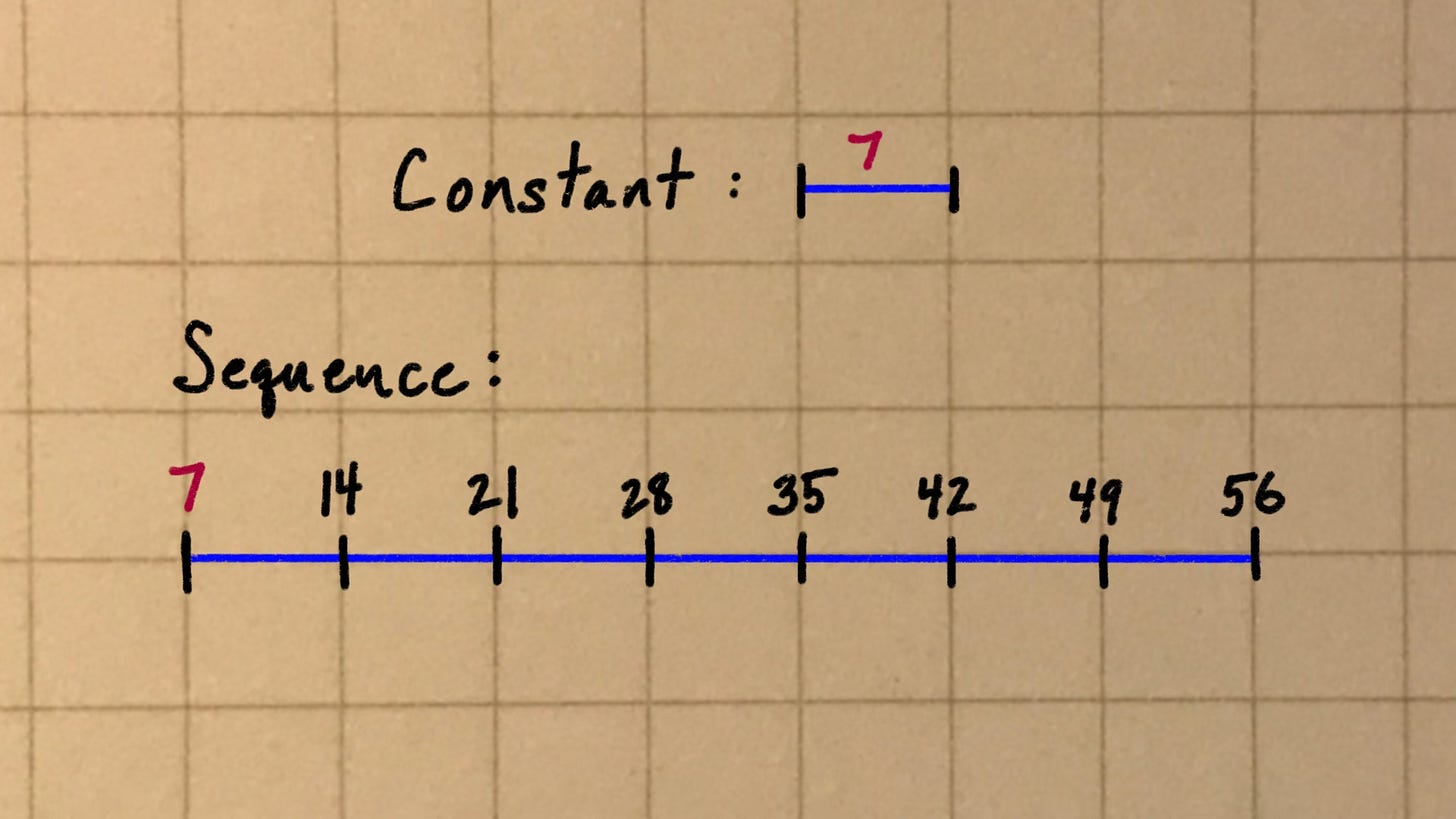
A “harmonic” sequence is just one kind of arithmetic sequence: specifically, one where the constant is the same as the first number in the sequence.
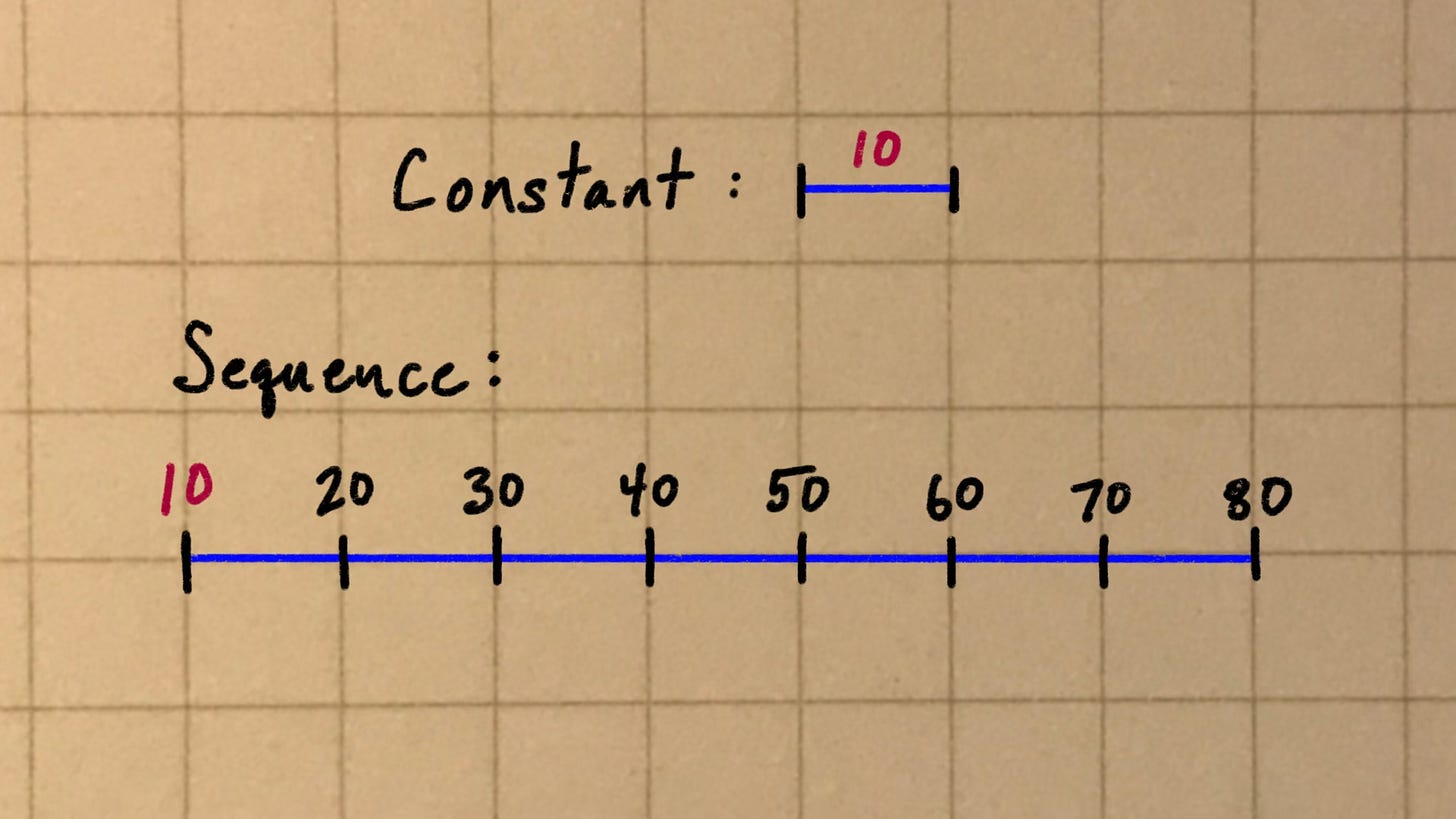
The sequence above is harmonic, and so are these:
Each successive number in the sequence is called a “partial,”1 and the first partial is also known as the “fundamental.”
So: that first number is simultaneously the fundamental, the first partial, and the constant between each successive partial. I love how that works, it’s tidy. 🧹
You only need to specify the fundamental to define a unique harmonic series. Just say “the harmonic series from 10” or “the harmonic series from 63.” There are as many unique harmonic series as there are numbers, which is to say… an infinite number.
The series continues: from the fundamental to forever.
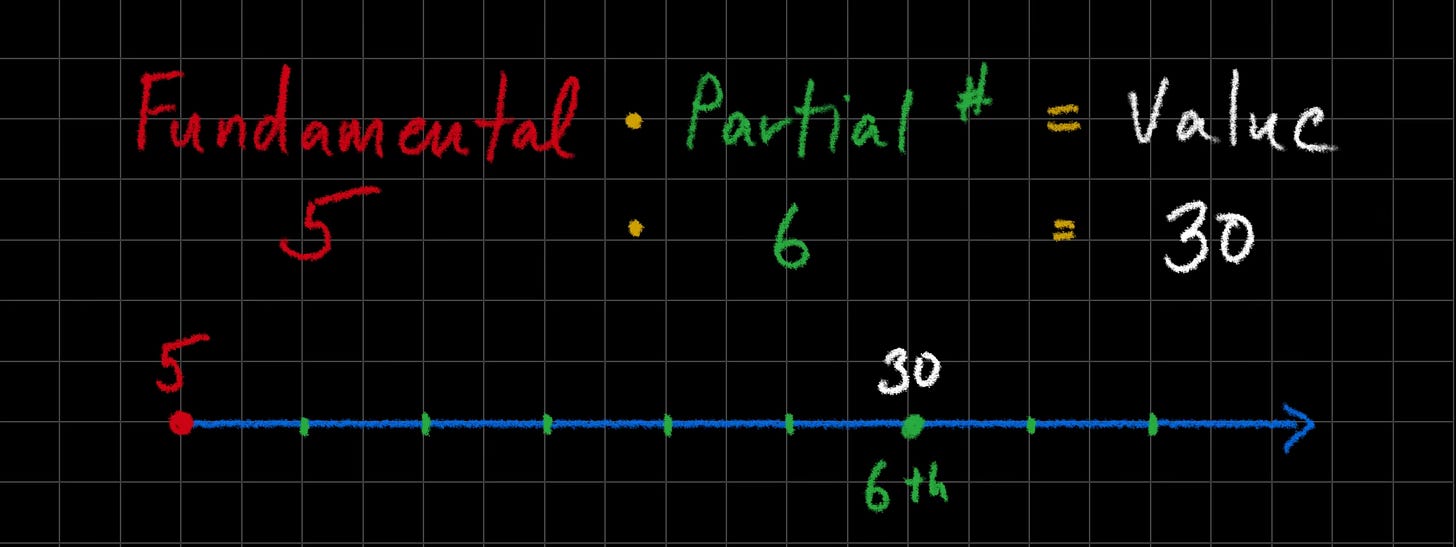
Want to find the value of a particular partial? Little equation: multiply the fundamental by the partial number:
That’s it — that’s about all the math you really need to start exploring how the concept of a harmonic series (or sequence)2 can apply to music, and to the world: just start applying the numbers of the sequence to something specific: length, speed, pressure, etc. Beautiful things start to appear.
🖼️ Right picture, wrong frame
And yet, if you’re like me, you were first introduced to “the harmonic series” in a music theory class textbook. It was probably treated as a sidebar to 20th century music and squeezed into a conceptually tangled mess of western staff notation, equal-tempered tuning, and “cents”:
Given the simplicity of the concept, I would have expected a pattern: a simple formula that could be used to derive the sequence indefinitely. But there is no pattern here — learning to recite this series would mean memorizing it term-by-term. It’s giving “pi to the 17th digit.”
When I saw this diagram in my college music theory class, my eyes crossed and I just went ahead and assumed it was none of my business… there’s no way a diagram this clumsy could be the musical depiction of such a simple and elegant mathematical concept. No, I thought, this clearly has nothing to do with me. And it obviously wasn’t going to sound like anything remotely musical:
Well… that was unexpected!
Ok now I’m interested. But if this is a harmonic series, what’s the constant? The distances between the 17 notated pitches on this staff (and how my ears perceive those differences) are for sure not constant: they keep getting smaller and smaller, and by strangely complicated combinations of “intervals” and “cents.”
That’s because notation evolved to reflect how our ears perceive those distances. We can get into that later — but within the far simpler framework of speeds of vibration, those differences are still constant:
The fundamental is a vibration of 55 times per second, and each successive note is vibrating that much faster than the one before it.
Here’s the exact same exact sequence, this time expressed in this simple mathematical framework:
Turns out there’s nothing inelegant about the harmonic series — what’s inelegant is squeezing it into the wrong framework. That framework, the language of our western system of tuning and notation, was simply not designed to describe it clearly.
So it’s a shame, but not surprising, that this beautiful and fundamental concept is barely touched upon in western music theory. After all, if your language doesn’t have a word for “blue”… why bother trying to describe the sky?
Here’s an excerpt for today:
🌌👨🏻🔬 Professor H at Twilight
This is an excerpt from True Stories & Rational Numbers — an album-length work for four pianos that I created during a multi-year process of thinking deeply about how we perceive the harmonic series on the separate scales of pitch, rhythm, tempo, and structure.
The most important figure in my own journey through this field of music cognition is the late 19th century physician and physicist Hermann von Helmholtz. His book On the Sensation of Tone made me consciously aware of the connection between music and physiology.
Fascinated by this rational, cognition-based approach that was never made available to me when I studied music, I sought to learn more about this “Professor H”… mainly from one epic biography (Helmholtz, A Life in Science — David Cahan):
He made staggering achievements in multiple scientific fields throughout his life, reflecting an immensely sustained focus and relentless work ethic.
He was a widower at a relatively early age. He had a turning point in his life when he met his second wife Anna, who was a salonniere — she turned their home into a weekly meeting-point for the elite of late 19th century intellectuals, naturalists, and academics. She also translated his scientific works.
They visited America together late in his life, to represent Germany at the International Electrical Congress (and boy did they have some parties)… the trip was a success, until he apparently bonked his head on the boat ride home, and was never quite the same.
Not the world’s most interesting guy, and yet I got weirdly fixated by the rationality of a person who could approach music how he did… so unlike the typical “music theorist.”
I kept trying to imagine what his life was like.
You know that thing where you project your own emotional world onto other people, particularly those you don’t actually have access to? When it comes to Helmholtz, I project super hard: I imagine he lived his early life in a state of rigid anxiety, scared to expose himself to the world and preferring to lock himself in a room with his pursuits. I picture a workaholic, terrified of facing even a single day without an all-consuming sense of purpose.
In my mind, Hermann tried to go to that house party once in college but only made it to the front door. Did I ever do that? Maybe. He was afraid of any situation that included new people. “Don’t worry Hermann, there won’t be anyone there you don’t know,” his friends would say… he still disappeared before anyone realized he was there.
And then I imagine Anna… a brilliant and gentle soul with all the confidence and self-assuredness Hermann never had, gradually introducing her world to him. She encourages him to open up to experience and let go of being so afraid. He exhales. His white-knuckle grip on all that is true and rational softens, bends… and he starts to notice the physical world of sensation.
Professor H at Twilight is my own little fan-fiction vision of Hermann and Anna on their way home from America. He is drifting off into senility, finally letting go of all his rigidity and obsessiveness and basically just experiencing all the sensations he spent his life intellectualizing. And Anna (reprise) is my image of her alone, once he's gone.
🧬⏱️ A harmonic series of tempos
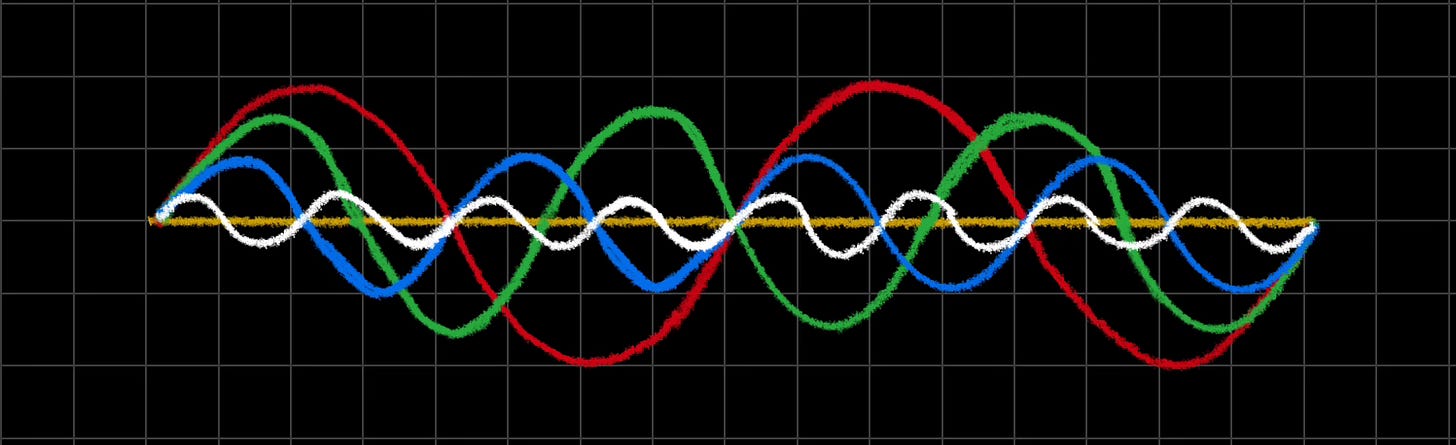
Although the harmonic series is usually described in music as a series of pitches, the concept I have returned to again and again is broader: I imagine it as a series of rates. This includes pitch, but also dips down into the slower scale of rhythm and tempo.
The video at the top of this article is that idea, visualized. The very bottom layer is the fundamental: pulses occurring at a tempo of 2 beats per minute.3 The tempo of each successive layer is 2 BPM faster than the one below it. So: it’s a harmonic sequence up from 2 BPM. The very top layer is the 85th partial: a rate of 170 BPM (2 * 85) .
This creates the effect of the tempo simultaneously expanding and contracting horizontally.
At the same time, each respective layer is also expressed as pitch: same relationships between partials, different scale of speed (much faster). We perceive this as waves of pitch: many upward and downward vertical motions that seem to be happening simultaneously.
Mathematically, pitch and tempo are two ends of the same scale, but our modes of perception separate them.
This is the compositional idea I used to create the last images of Professor H as he fades away in True Stories… I started with the full compliment of partials as in the video above, and I started intuitively subtracting from it. I removed entire horizontal layers (partials), I selectively removed individual notes, I isolated some of those interesting sloping shapes by muting the notes around them. I also played with relative loudnesses and duration, and eventually I had achieved this sort of “broken grandfather clock” effect: the precision of the whole mechanism is still there, but individual elements are starting to go missing, be forgotten, fade away.
Thank you for taking the time to speak with me today, 🗞️ Here’s a pamphlet with more information: I’m encouraging young folks like you to consider the grand future that The Harmonic Series holds out to us. Does that sound good to you?
Spread The Word!
Subscribe for free:
🙂 Real confessions: I write these articles because I’m hoping they might make you want to explore my music. Oh look there’s the album below! Click through to get True Stories & Rational Numbers (and all my other music) on vinyl, cd, or streaming.
☆ Thanks as always to Daniel Powell and Sonic Couture for the support, and for creating the Hammersmith Piano, which was used to create every musical example above, and which has proven endlessly fruitful in my own music for the past 5 years.
You might have heard of “overtones” — feel free to disabuse yourself of this word and strike it from your mental record forever. It will only cause you pain.
I try to tread carefully with my use of “series” vs “sequence.” In mathematics, a “series” is actually the sum of all the numbers in a sequence. A “harmonic series,” as used in music, is infinite: theoretically, the sequence goes on forever, so numerically the value of the “series” is infinity. We can represent that infinity as an equation (less meaningful in music), or just as a sequence of terms with the little “…” at the end to show it goes on forever (that’s what I do). So when I use “sequence,” it’s to describe a finite list of numbers. When I talk about a “harmonic series,” I’m referring to The Whole Infinite Thing.
In case you’re fact-checking, it’s actually 1.875 BPM. I recorded this with the tempo set a hair slower and didn’t feel like remaking the video. 🤷♂️